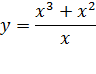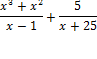Профилактика затруднений школьников при обучении математике на примере темы "Уравнения с переменной в знаменателе"

изначально сказать, что функция определена только на своей области определения, а значит, в 0 не существует.

При построении графика функции (табличном) шаг таблицы в окрестности точки 0 брать меньше.

С учетом этих замечаний можно выполнить задания вида:

Выражения с переменными

Заданий на нахождение области определения в этой теме достаточно, однако стоит обратить внимание на обоснование запрета деления на 0, а также на задания вида: Сравните множества значений выражений

Функция «обратная пропорциональность»

К моменту изучения этой функции учащиеся должны знать про особенность её области определения (при необходимости можно повторить, решая задания на определение множества значений функции с переменной в знаменателе), что позволяет правильно начертить график (ОУ - асимптота). Изучение её поведения в окрестности точки 0, построение графика позволяют получить наглядное представление о проблеме деления на 0.

Решение дробных рациональных уравнений

Эта тема является основной в изучении данного вопроса, при соблюдении вышеуказанных рекомендаций, её изучение не должно вызвать трудностей, однако, перед началом изучения необходимо повторить следующие факты:

Обе части уравнения можно умножить или разделить на одно и то же не равное 0 число.

К обеим частям уравнения можно прибавить одно и то же число.

Условие равенства дроби 0: дробь равна 0, когда её числитель равен 0, а знаменатель не равен 0.

Далее следует рассмотреть алгоритм решения рационального уравнения с проверкой изменения множества допустимых значений на каждом шаге.

Есть 2 способа решения таких уравнений: традиционный и способ, использующий равенство дроби 0. (см. Глава 1)

Традиционный способ прост и алгоритмичен, но решение уравнений такого вида традиционным способом «отбрасывания знаменателя», который заключается в том, что левая и правая части уравнения представляются в виде дробей, а затем умножаются на общий знаменатель дробей неудачно. Учащиеся плохо понимают, на чем основано «отбрасывание знаменателя», а приобретенное умение переносят на тождественные преобразования дробных выражений, что влечет за собой грубейшие ошибки.

Использование условия равенства дроби нулю или условия равенства двух дробей позволяет добиться более глубокого понимания существа дела и значительно снизить число ошибок, допускаемых учащимися при решении уравнений указанного вида.

Читайте также:

Структурно-логическое содержание обучения - основа компьютерной технологии обучения
Для определения степени обучаемости студентов по каждой учебной дисциплине выделяют объем знаний, которые необходимы для усвоения согласно учебной программе, что составляет базовый объем знаний. Базовые знания представляют минимум государственного образовательного стандарта. Но и среди базовых знан ...

Опыт использования компьютерный технологий для обучения информатике незрячих детей
Современные информационные образовательные технологии могут быть использованы для предоставления образовательных услуг людям с ограниченными возможностями, например, незрячим и слабовидящим. Следует отметить, что компьютерные технологии в данном случае рассматриваются не только и не столько как пре ...

Педагогические условия и особенности формирования познавательного интереса младших школьников в учебной и внеучебной деятельности
Познавательный интерес проявляется в эмоциональном отношении школьника к субъекту познания. Л.С. Выготский писал: «Интерес – как бы естественный двигатель детского поведения, он является верным выражением инстинктивного стремления, указанием на то, что деятельность ребенка совпадает с его органичес ...