Профилактика затруднений школьников при обучении математике на примере темы "Уравнения с переменной в знаменателе"

Необходимо подчеркнуть, что здесь для нас существенным является тот факт, что выражение g(х) имеет смысл при любом х. В общем случае уравнение вида равносильно системе

Например, уравнение

равносильно системе

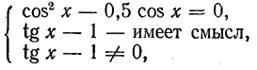т. е. cистеме

Следует заметить, что при решении системы 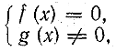где

f(х) и g(х) — некоторые многочлены, вовсе не обязательно находить множество значений х, при которых Достаточно, найдя

корни уравнения , проверить, удовлетворяют ли они условию

В учебниках метод решения уравнений вида , где

f(х) и g(х) — целые выражения, разъясняется на примере уравнения

,

равносильного системе

.Учащиеся

не могут найти множество значений х при которых х 3— х — 1200, но этого и не требуется для решения системы. Непосредственная подстановка убеждает их, что из двух корней уравнения х2 — 5х = 0, равных 0 и 5, только первый удовлетворяет условию Значит, рассматриваемая система, а следовательно и уравнение

,

имеет единственное решение — число 0.

При решении уравнения вида r(х) = р(х), где r(х) и р(х) — рациональные выражения, можно не сводить его к уравнению r(х) — р(х) = 0, а представить выражения r(х) и р(х) в виде дробей с одинаковыми знаменателями. Если при этом не выполнялись тождественные преобразования, которые могут привести к нарушению равносильности, то получится уравнение вида

,

где т(х), п(х), q(х) — целые выражения, равносильные уравнению r(х) = р(х). Уравнение указанного вида равносильно системе

Равносильность этих предложений можно доказать, опираясь на свойство числовых дробей: дроби с одинаковыми знаменателями равны тогда и только тогда, когда их числители равны, а общий знаменатель отличен от 0 (выражение q(х) имеет смысл при любом значении х).

Читайте также:

Учебные функции ролевых игр
А теперь давайте рассмотрим ролевую игру с точки зрения ее других основных характеристик. В условиях обучения ролевая игра - это прежде всего речевая деятельность, игровая и учебная одновременно. С точки зрения учащихся ролевая игра - это игровая деятельность, в процессе которой они выступают в опр ...

Имущество, хозяйственная и финансовая деятельность ДДТ
7.1 Имущество ДДТ составляют основные и оборотные средства, финансовые ресурсы, которые принадлежат ему на праве оперативного управления, закрепленные за ДДТ отделом имущественных отношений Бардымского муниципального района; 7.2 Источниками образования имущества ДДТ являются: • земля, здание ДДТ; • ...

Специфика проявления внимания у младших школьников на уроках физической культуры
Трудно переоценить значение внимания для эффективности занятий физическими упражнениями. Ничто не может быть воспринято и усвоено без сосредоточения психической деятельности – без внимания. На уроках физической культуры следует использовать все типы внимания ученика. Если на уроке преобладает произ ...