Профилактика затруднений школьников при обучении математике на примере темы "Уравнения с переменной в знаменателе"

выражение 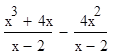дробью и сократив эту дробь, мы получим уравнение х (х - 2) = 0, (5) не равносильное уравнению (4). Действительно, число 2 удовлетворяет уравнению (5), но не удовлетворяет уравнению (4).

Нарушение равносильности произошло за счет того, что мы выполнили тождественное преобразование, приводящее к выражению с более широкой областью определения: выражение определено при х2, а выражение х (х — 2) — при любом значении х.

Пример 2. В уравнении

(6)

заменим разность 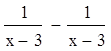числом 0. Получим уравнение

(7)

Уравнение (7) не равносильно уравнению (6), так как существует такое значение переменной х (число 3), которое удовлетворяет уравнению (7), но не удовлетворяет уравнению (6).

Равносильность нарушена в связи с тем, что область определения выражения 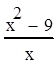шире, чем область определения выражения

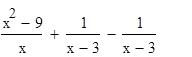
Если же при замене разности r (х) — р (х) рациональных выражений, хотя бы одно из которых дробное, дробью , где f (х) и g (х) — многочлены, были выполнены только те тождественные преобразования, которые не меняют области определения выражения, то получится уравнение равносильное уравнению r(х) — p(х) = О, а значит, и уравнению r(х) = р(х).

Так для уравнения (4) равносильным является уравнение

.

Для уравнения (6) равносильным является уравнение

т. е. уравнение

Заметим, что в том случае, когда в ходе выполнения тождественных преобразований область определения выражения расширилась, предложением, равносильным уравнению r(х) — р(х) = 0, будет являться система, составленная из уравнения и ограничений, накладываемых на х в связи с изменением области определения. Например, для уравнения (4) равносильным предложением является система

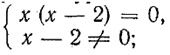
для уравнения (6) — система

Для решения уравнения вида 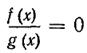где f(х) и g(х) — некоторые многочлены, используется условие равенства дроби нулю: дробь равна нулю тогда и только тогда, когда ее числитель равен нулю, а знаменатель отличен от нуля. Поэтому уравнение указанного вида равносильно системе

Читайте также:

Методы диагностики особенности воспитания единственного ребенка в семье на констатирующем этапе эксперимента
В первой главе мы теоретически обосновали особенности воспитания единственного ребенка в семье младшего школьного возраста. Исходя из этого, нами было проведено исследование, в ходе которого необходимо осуществить диагностику, которая позволяет выявить, что если семья воспитывает единственного ребе ...

Понятие «модель» в социально-педагогическом исследовании
Термин «модель» широко используется в различных сферах человеческой деятельности и имеет множество смысловых значений. Под «моделью» понимается такой материальный или мысленно представляемый объект, который в процессе исследования замещает объект-оригинал так, что его непосредственное изучение дает ...

Национальная нетерпимость и ее причины
Люди обыкновенно думают, что их восприятия и представления о вещах совпадают, и если два человека воспринимают один и тот же предмет по-разному, то один из них определенно ошибается. Однако психологическая наука отвергает это предположение. Восприятие даже простейшего объекта - не изолированный акт ...