Профилактика затруднений школьников при обучении математике на примере темы "Уравнения с переменной в знаменателе"

Упростив уравнение (2), получим квадратное уравнение

Его корни – числа -2 и 5.

Проверим, являются ли они корнями уравнения (1). При 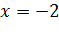общий знаменатель не обращается в 0. Значит, число -2 – корень уравнения(1).

Итак, корнем уравнения (1) служит только число -2.

Вообще, при решении дробных уравнений целесообразно поступать следующим образом:

Найти общий знаменатель дробей, входящих в уравнение;

Умножить обе части уравнения на общий знаменатель;

Решить получившееся целое уравнение;

Исключить из его корней те, которые обращают в 0 общий знаменатель.

Метод, использующий равенство дроби 0.

Начнем с примера. Пусть требуется решить уравнение

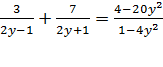(1)

Перенесем выражение 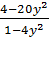в левую часть уравнения с противоположным знаком, т. е. прибавим к обеим частям уравнения по 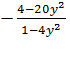и разность 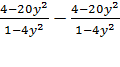в правой части уравнения заменим нулем. Получим уравнение

(2)

Может ли при переходе от уравнения (1) к уравнению (2) произойти потеря или приобретение корней?

Очевидно, что так как разность 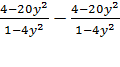тождественно равна 0 на множестве тех значений у, при которых то мы могли бы приобрести новые корни за счет значений у, обращающих в нуль выражение Но они не могут служить корнями уравнения (2), так как при этих значениях выражение , входящее в качестве слагаемого в левую часть уравнения (2), теряет смысл.

Рассуждая аналогично, мы можем показать, что вообще уравнение r(х) = р(х), где r(х) и р(х) — рациональные выражения, причем хотя бы одно из них дробное, равносильно уравнению r(х) —p(x)=0

Вернемся к рассматриваемому примеру. Представив теперь cумму дробей 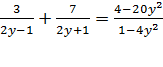в виде отношения двух многочленов, получим уравнение

(3)

Так как в результате преобразования суммы дробей в дробь мы получили выражение с той же областью определения и тождественно равное исходному выражению на этой области, то уравнение (3) равносильно уравнению (2), а следовательно, и уравнению (1).

Всякое ли преобразование дробного выражения r(х) — p(х) в дробь, числитель и знаменатель которой многочлены, позволяем от уравнения r(х) — р(х) = 0 перейти к равносильному уравнению вида 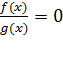, где f (х) и g (х) — многочлены?

Рассмотрим примеры.

Пример 1. Заменив в уравнении

(4)

Читайте также:

Кризисные явления в системе вузовского образования в России и задачи их преодоления
Как и любая реформируемая система, система образования Российской Федерации испытывает определенные трудности. Например, проблема равенства доступа к образованию, которая имеет два основных аспекта: 1) обеспечение доступа каждого человека к базисному образованию, необходимому для эффективного функц ...

Этапы формирования государственной политики развития образования в России
Образование в древней Руси На Руси учебные заведения именовались училищами: слово школа вошло в обиход начиная с XIV века. Уже в первой половине XI века нам известны дворцовая школа князя Владимира в Киеве и школа, основанная Ярославом Мудрым в Новгороде в 1030 году. Содержание образования, как и в ...

Использование интеграции содержания учебных предметов для формирования ЗОЖ
Для успешного проведения интегрированных уроков необходимо создать атмосферу заинтересованности и творчества. В реализации межпредметных связей, при изучении биологии, условно можно выделить два блока процессов: актуализация и конкретизация. Под актуализацией мы понимаем создание на уроке такой сит ...